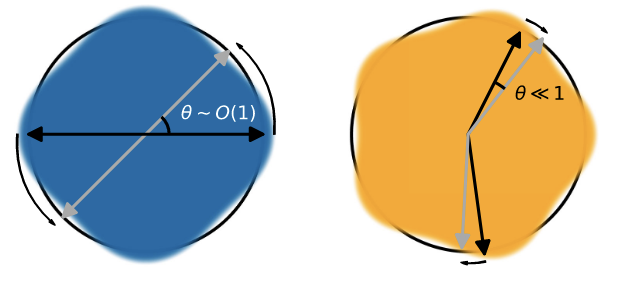2D Fermi Liquids | Eric Nilsson

In clean, two-dimensional materials, the electrons can reach a hydrodynamic transport regime, flowing around obstacles like water. However, the kinematics of electrons in 2D are heavily constrained by the scattering phase space set by the Fermi surface. By expanding Fermi surface deformations into angular harmonics, one may classify that even-parity deformations can decay through head-on collisions, leading to a standard Fermi liquid decay rate $\gamma_{\text{even}} \sim T^2/T_F$. Odd-parity deformations instead have to rely on repeated small-angle scattering events assited by the thermal broadening, leading to a thermally supressed decay rate $\gamma_{\text{odd}} \sim T^4/T_F^3$.

That odd and even Fermi surface deformations relax on parametrically different timescales hints at the existence of a novel transport regime in between ballistic and hydrodynamic flow: a “tomographic” regime, consisting of hydrodynamic modes, in addition to the long-lived odd-parity modes.

Together with my collborators we have detailed a method of exactly diagonalizing the collision integral in the Boltzmann equation, including the effects of the Coulomb interaction between the electrons (Nilsson et al., 2025). This allowed us to completeley characterize the mode spectrum, and we found that the odd-parity effect in the decay rates extends to temperatures as large as $T = 0.15 T_F$. Furthermore, there is only a small number of long-lived odd-parity modes, with an infinite number of remaining modes that show standard Fermi-liquid scaling, and the ratio between the odd- and even-parity lifetimes is tunable with the Coulomb interaction strength.

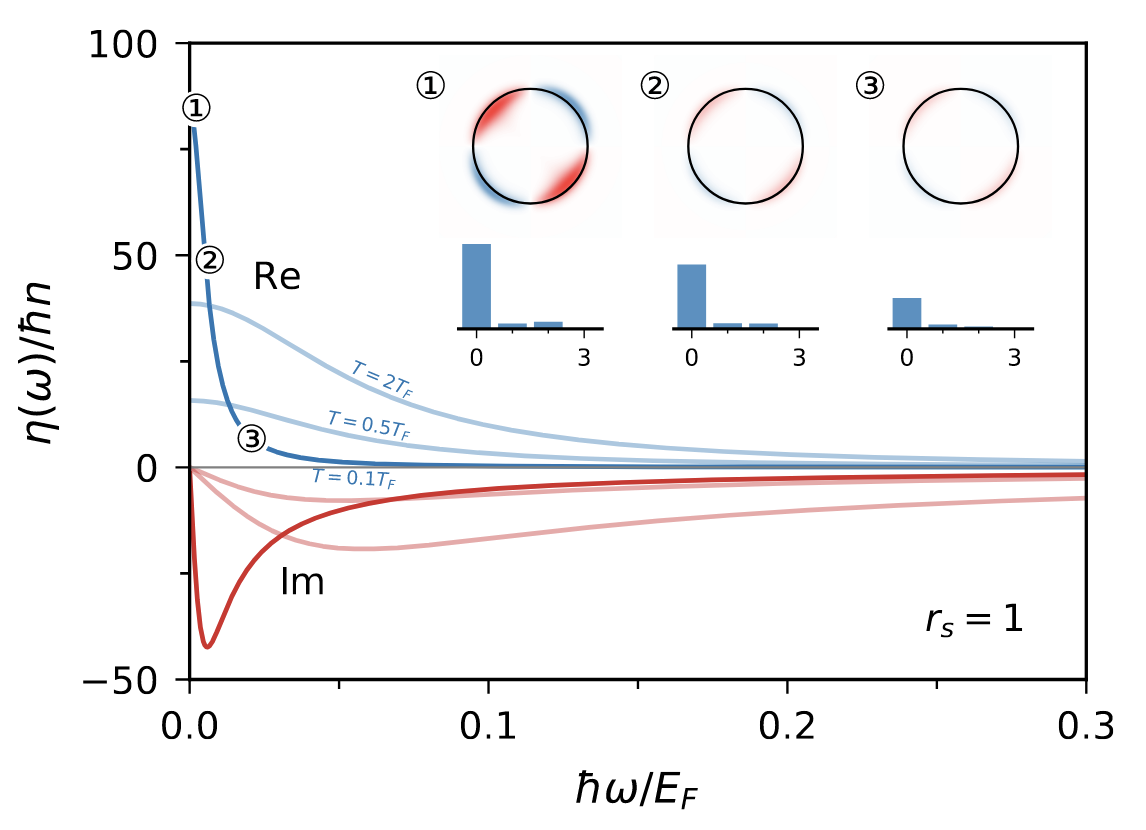
We also applied the results of the exact diagonalization to compute transport coefficients; in particular the shear viscosity (Gran et al., 2023). Valid at all temperatures, we are able to describe the response beyond the asymptotic low-temperature limit, where perturbative approaches exist. Even in this low-temperature limit, there is a nonanalytic exchange contribution to the shear viscosity, highlighting the need for a full nonperturbative solution of the Fermi liquid equation.

References

PRX
Nonequilibrium Relaxation and Odd-Even Effect in Finite-Temperature Electron Gases

Eric Nilsson, Ulf Gran, and Johannes Hofmann

Physical Review X, Oct 2025

Abs DOI arXiv Bib HTML

Pauli blocking in Fermi liquids imposes strong phase-space constraints on quasiparticle lifetimes, leading to a well-known quadratic-in-temperature decay rate of quasiparticle modes at low temperatures. In two-dimensional systems, however, even longer-lived modes are predicted (dubbed “odd-parity” modes) that involve a collective deformation of the Fermi distribution. Here, we present an efficient method to evaluate the full spectrum of relaxational eigenmodes of a Fermi liquid within kinetic theory. We employ this method to study the experimentally relevant case of a Fermi liquid with screened Coulomb interactions and map out the decay rates of quasiparticle modes beyond the asymptotic low-temperature limit up to the Fermi temperature, thus covering the entire temperature range of typical experiments. We confirm the existence of anomalously long-lived odd-parity modes and provide a comprehensive classification and detailed analysis of the relaxation spectrum. In particular, we find that (i) the odd-parity effect in the decay rates extends to temperatures as large as T = 0.15 T_F, (ii) there is only a small number of long-lived oddparity modes, with an infinite number of remaining modes that show standard Fermi-liquid scaling, and (iii) the ratio between the odd- and even-parity lifetimes is tunable with the Coulomb interaction strength, in addition to temperature, which reflects a difference in the microscopic relaxation mechanism of the modes. Our findings provide a comprehensive description of the nonequilibrium relaxation behavior of twodimensional electron gases and bridge a significant gap in our understanding of these systems.
@article{nilsson_nonequilibrium_2025, pubtype = {paper}, title = {Nonequilibrium {{Relaxation}} and {{Odd-Even Effect}} in {{Finite-Temperature Electron Gases}}}, author = {Nilsson, Eric and Gran, Ulf and Hofmann, Johannes}, year = {2025}, month = oct, journal = {Physical Review X}, volume = {15}, number = {4}, pages = {041007}, issn = {2160-3308}, doi = {10.1103/ly37-5gdw}, urldate = {2025-10-25}, langid = {english}, publisher = {aps}, eprint = {2405.03635} }
arXiv
Shear Viscosity in Interacting Two-Dimensional Fermi Liquids

Ulf Gran, Eric Nilsson, and Johannes Hofmann

Dec 2023

Abs arXiv Bib

In interaction-dominated two-dimensional electron gases at intermediate temperatures, electron transport is not diffusive as in the conventional Drude picture but instead hydrodynamic. The relevant transport coefficient in this regime is the shear viscosity. Here, we develop a numerically exact basis expansion to solve the Fermi liquid equation, and apply it to compute the shear viscosity of the electron gas with screened Coulomb interactions. Our calculations are valid at all temperatures and in particular describe the response beyond the asymptotic low-temperature limit, where perturbative approaches exist. We show that even in this low-temperature limit, there is a nonanalytic exchange contribution to the shear viscosity, highlighting the need for a full nonperturbative solution of the Fermi liquid equation. We hope that the techniques developed in this work will serve as a platform to determine the response of interacting Fermi liquids.
@misc{gran_shear_2023, pubtype = {preprint}, title = {Shear Viscosity in Interacting Two-Dimensional {{Fermi}} Liquids}, author = {Gran, Ulf and Nilsson, Eric and Hofmann, Johannes}, year = {2023}, month = dec, number = {arXiv:2312.09977}, publisher = {arXiv}, urldate = {2023-12-20}, archiveprefix = {arXiv}, copyright = {All rights reserved}, langid = {english}, eprint = {2312.09977}, }